1.オイラー法
常微分方程式の数値解法の一つ
数学的に理解しやすく、プログラム的にも簡単
数値解析の初歩的な学習問題としてよく取りあげられる
常微分方程式に初期条件を与えることで,
未知数を含まない形で書けるような問題を「初期値問題」と呼び
微分方程式の数値解法は初期値問題を解くことを目的とする
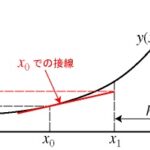
x0 から x1 のような幅が刻み幅に相当する区間において,
傾きが f(x0,y0) で一定であると仮定して近似解を求める
傾きは一定では無い,近似が正確となりうるのは,h→0 の極限のみ
2.ガウスの消去法
連立一次方程式を解くアルゴリズムの一つ
拡大係数行列を行基本変形することで解を求める
掃き出し法とも呼ばれる
ガウスの消去法は
前進消去(文字を1つずつ消していく操作)
方程式の定数倍を他の方程式に加えることで文字を順番に消していく
元の式

一番目の式を −1 倍し二番目の式に加える
一番目の式の −2 倍を三番目の式に加える
計算する(x1を消す)

二番目の式を 1/3 倍し三番目の式に加える
計算する(x2を消す)

これで「目標の形」x3=2が求まる
後退代入(1成分ずつ答えを求めていく操作)
後ろの式から順番にたどっていき,1つずつ変数の値を求めていく
x3=2を二番目の式に代入する −3*x2 + 5x2 = 1
x2=3
x2=3、x3=2を一番目の指揮に代入する x1 + 2*3 -2*2 = 3
x1 = 1
これでx1 = 1、x2=3、x3=2が求まる
3.シンプソン法
区分求積法
より次数の高い関数で近似できた方が誤差が減少する可能性がある
2次関数を表現する場合には3点を利用する必要があり,
2つの区分を利用する必要がある
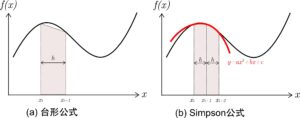
| $$ 3点を以下のように考える x_{0}、x_{1 }、x_{2 },その関数値をf_{0}、f_{1 }、f_{2} $$ |
| $$ 2次関数がx_{0}でf_{0}を通ることから, $$ |
| $$ 2次関数の係数をa,b,c(=f_{0})とし f_{x}=a(x−x_{0})^2+b(x−x_{0})+f_{0} $$ |
| 同時に他の2点を通るということから |
| \begin{equation} f_1 = a(x_1-x_0)^2+b(x_1-x_0)+f_0 \end{equation} |
| \begin{equation} f_2 = a(x_2-x_0)^2+b(x_2-x_0)+f_0 \end{equation} |
| $$ x_1-x_0=h、 x_2-x_0=2hを代入して計算すると $$ |
| 以下のようなaとbに関する連立方程式となる |
| \begin{equation} \large a=\frac{f_0-2f_1+f_2}{2h^2}、\quad b = \frac{-3f_0+4f_1-f_2}{2h} \end{equation} |
| 元の2次間数 |
| \begin{equation} f(x) = a(x-x_0)^2+b(x-x_0)+f_0\label{fx} \end{equation} |
| $$ 関数をx_0、x_2で積分する $$ |
| \begin{eqnarray} I&=&\int_{x_0}^{x_2}\left( a(x-x_0)^2+b(x-x_0)+f_0 \right)dx \nonumber \\ &=& \left[ \frac{1}{3}a\left( x-x_0 \right)^3 + \frac{1}{2}b\left( x-x_0 \right)^2 +f_0x\right]_{x_0}^{x_2}\nonumber \\ &=& \frac{1}{3}a\left( x_2-x_0 \right)^3 + \frac{1}{2}b\left( x_2-x_0 \right)^2 +f_0(x_2-x_0)\nonumber \\ &=& \frac{1}{3}\frac{f_0-2f_1+f_2}{2h^2}8h^3 + \frac{1}{2}\frac{-3f_0+4f_1-f_2}{2h}4h^2 +2f_0h\nonumber \\ &=& {\large \frac{h}{3}\left( f_0+4f_1+f_2 \right)} \end{eqnarray} |
4.ニュートン法
方程式の解を数値計算によって近似的に求める
ニュートン・ラフソン法とも呼ばれる
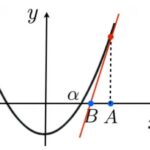
| 2次方程式 |
| $$ y=x^2-2 $$ |
| x=aにおける接線の方程式を求める |
| $$ y=2ax-a^2-2 $$ |
| y=0を代入 |
| $$ 0=2ax-a^2-2 $$ |
| $$ 2ax=a^2+2 $$ |
| $$ x=\frac{1}{2a}(a^2+2) $$ |
| $$ x=\frac{1}{2}(a+\frac{2}{a}) $$ |